Spirit graphs are meant to diagrammatically summarize the movements of spirits through the story. Here is an example.
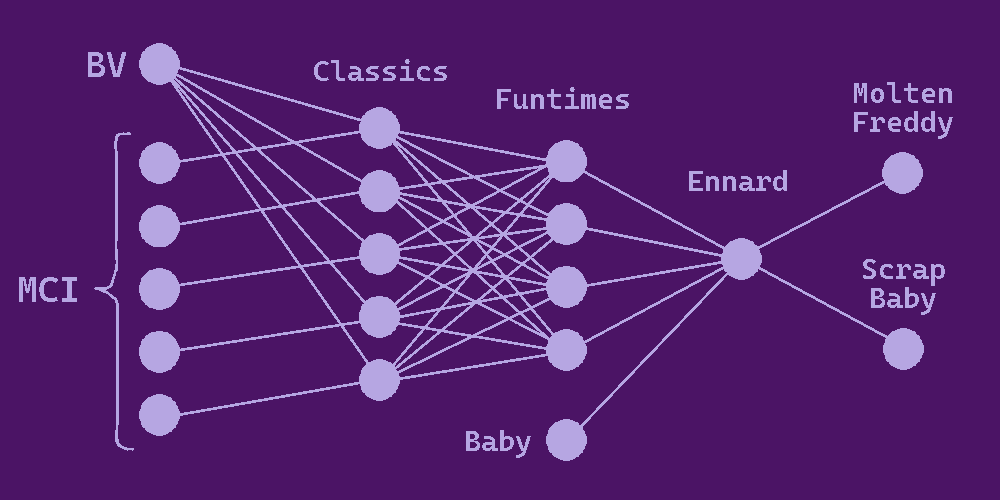
(Diagrams henceforth will be much sloppier than this.)
If you, the reader, just so happened to be familiar with applied category theory, it may or may not have been obvious to you that this seems to be a kind of "string diagram". I will very briefly explain what this means, as I understand. Here is a more in-depth overview, if you're interested.
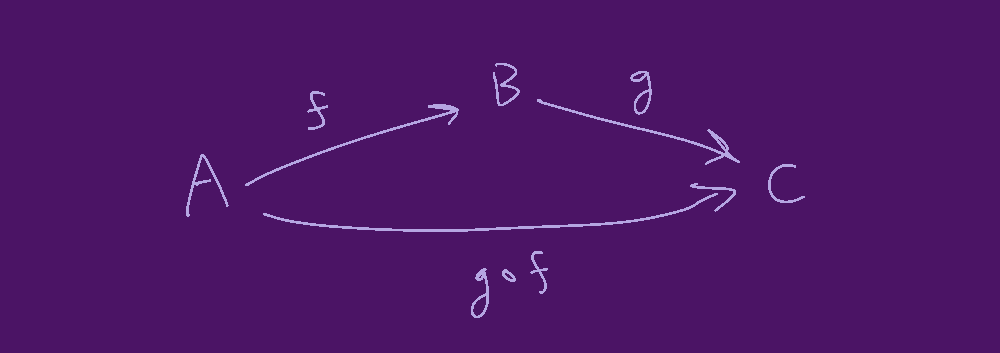
A category, in this context, is a collection of objects (\(A,B,C,\) etc) and morphisms (\(f,g,h,...\) etc). A morphism is an arrow or "mapping" between two objects, with a domain (source object) and codomain (destination object). For any two morphisms (say \(f\) and \(g\)) which connect end-to-end, there is another morphism (\(g \circ f \)) which is their "composition".1
Categories are often drawn with diagrams that look like this.
A monoidal category is a category where objects (say \(A\) and \(B\)) can be multiplied2: \(A \times B\).
In monoidal categories, morphisms can be drawn using string diagrams.
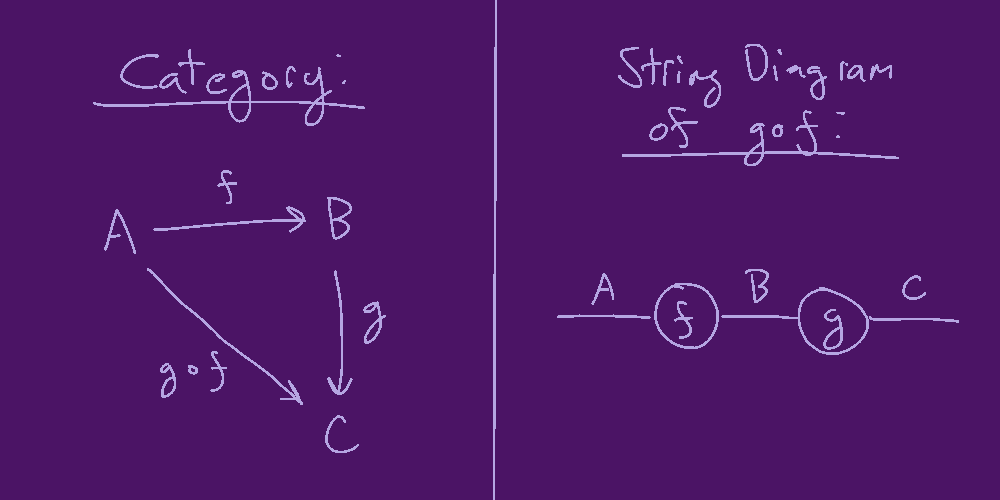
Running left to right, the string diagram treats objects as flows which are transformed by morphisms. Products are written with multiple adjacent lines.
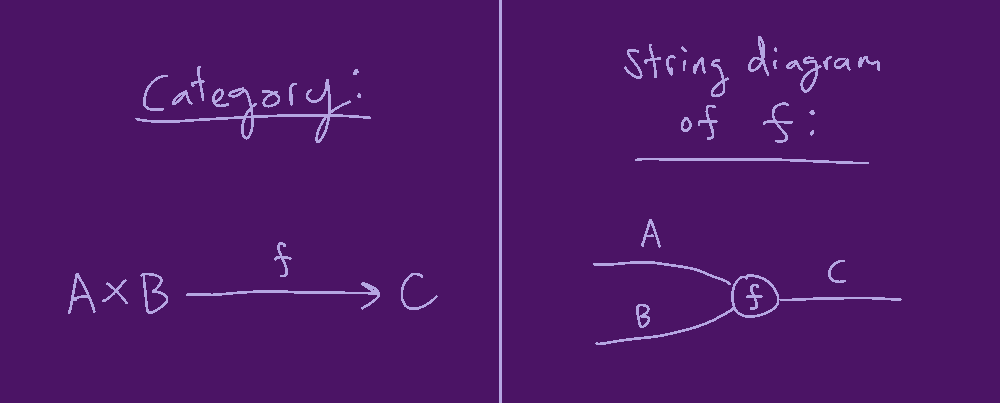
There are more technical details necessary for a rigorous treatment, but you've gotten the gist, so I'm going to go ahead and connect this to spirit graphs. My interest now is in reverse-engineering spirit graphs into their categorial form, to understand the contextual meaning of their components.
It seems there are multiple ways to rework spirit graphs to look like string diagrams. Here is one way which seems fairly cohesive to me.3
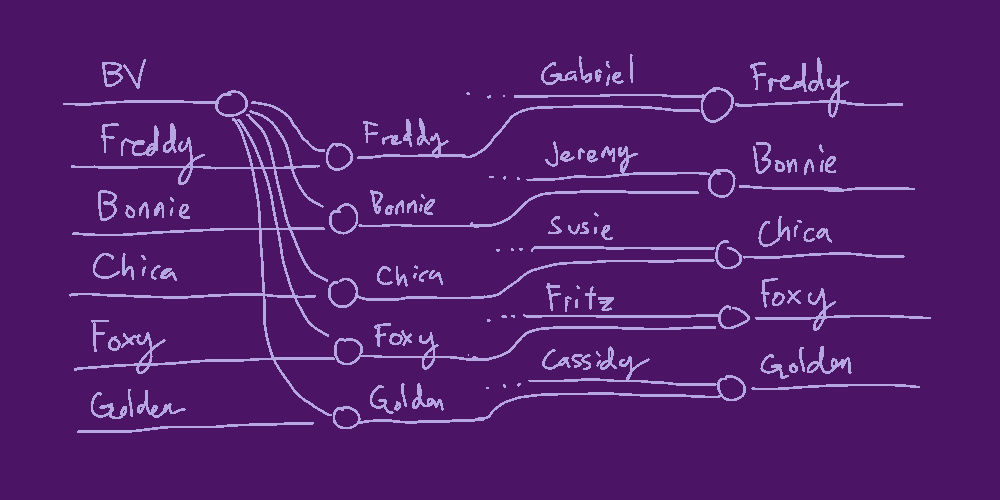
We see that objects are characters (people, animatronics, etc), and morphisms are hauntings. For example, a morphism of the form... \[ \text{Susie} \times \text{Chica} \to \text{Chica} \] ...represents the event of Susie coming to haunt Chica. The product can be read simply as "and", so this is a morphism which starts with Susie and Chica together, and ends with just Chica (haunted by Susie).
Naturally, splitting (breaking) takes the form: \[ \text{Person} \times \text{Vessel}_1 \times \text{Vessel}_2 \to \text{Vessel}_1 \times \text{Vessel}_2 \] ...with merging (putting back together) as: \[ \text{Vessel}_1 \times \text{Vessel}_2 \to \text{Vessel}_3 \] Note that the merging morphism doesn't represent haunting; rather, it represents the physical process of the vessels merging together. We can similarly write a morphism for physical splitting of vessels: \[ \text{Vessel}_1 \to \text{Vessel}_2 \times \text{Vessel}_3 \] ...which might also involve soul splitting, if \(\text{Vessel}_1\) happens to be haunted.
This way of handling things is intuitive in that each diagram will start with all the necessary components (people and vessels), which are then simply merged together in various ways. It is... a little messy, though. The diagram is cluttered with lines, and looks quite different from the original spirit graph. An alternative approach would be to allow haunting morphisms with the simpler form: \[ \text{Susie} \to \text{Chica} \] ...which allows redrawing the diagram as:

...which is a bit more faithful to the original graphs.
(Note that we cannot fully get rid of the old haunting morphisms, it seems, so long as we want to be able to put multiple souls in the same vessel.)
Using this simpler form, here's the full graph from the beginning, reformatted.
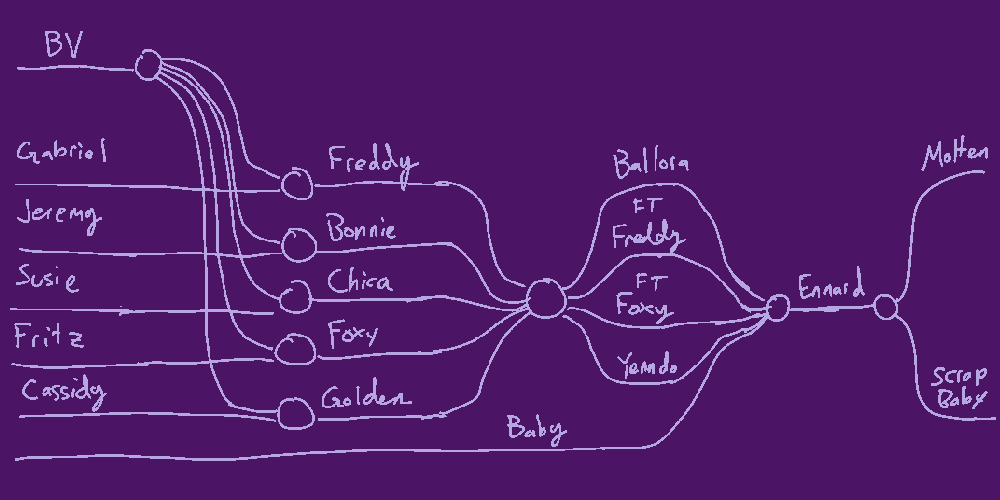
I will call this category "\(\text{FNaF}\)". It contains all FNaF characters (or collections of characters) as its objects, and as its morphisms all conceivable relations of haunting, or of physical transformation (eg Funtimes \(\to\) Ennard). A FNaF theory or AU takes the form of a particular morphism in this category, mapping some collection of characters to their vessels.
Is there any interesting insights which can be gleaned from all this? Well... I don't know. I don't know very much about monoidal categories, to be honest.
:p
- I'm skipping details that aren't important here- namely, that composition is associative, and that all objects have identity morphisms.
- ... with associativity and an identity element. \(\text{FNaF}\) is a symmetric monoidal category, meaning multiplication is also commutative: \(A\times B = B\times A\). Actually, these features are only needed up to isomorphism. But I will be ignoring that.
- Note that I have BV being put into the Classics before the MCI, here. Because I think that is likely what happens.